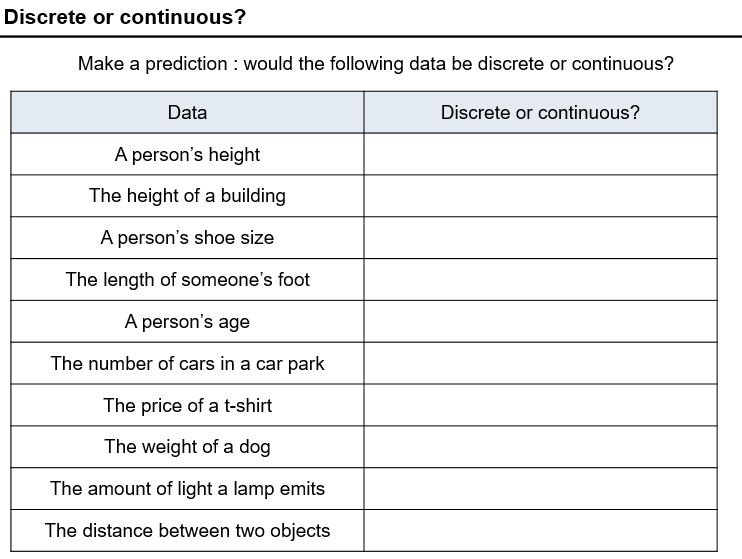
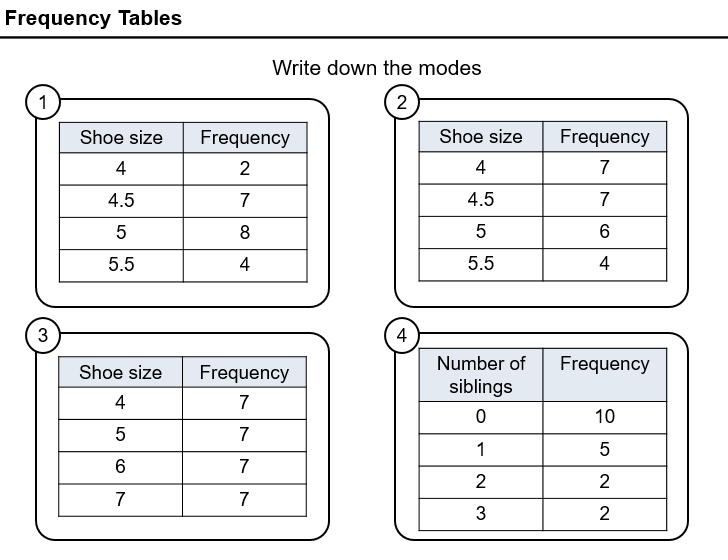
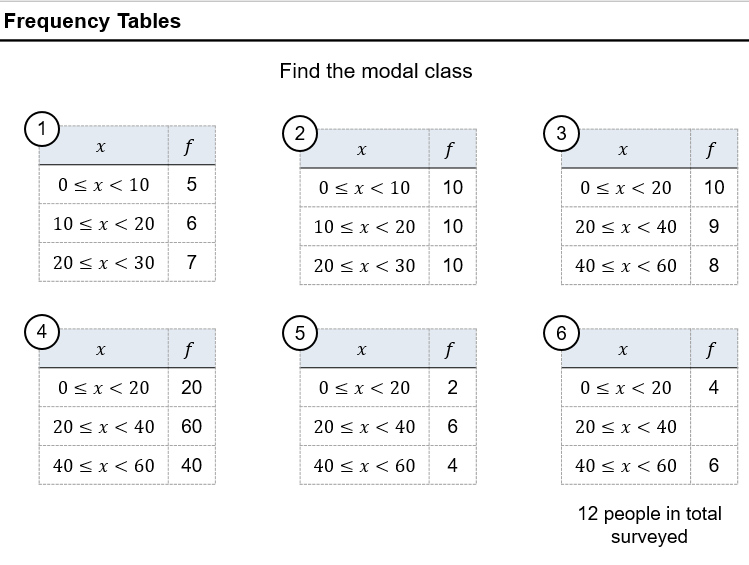
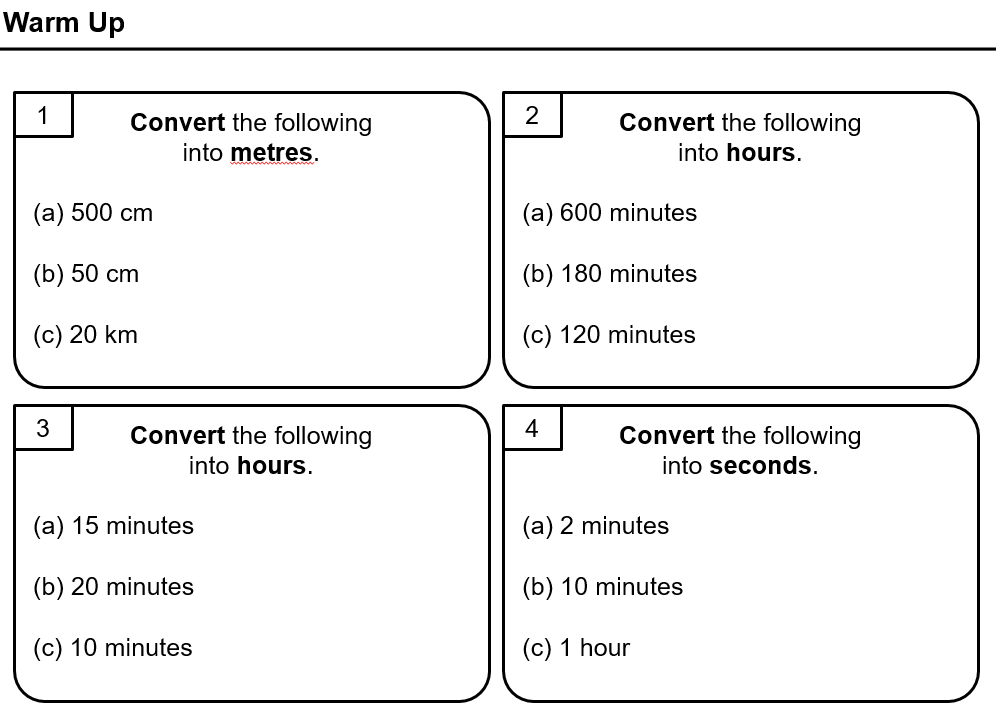
(As a side note, I’d really like to not use TES to host these resources at some point, but haven’t really found a better option).
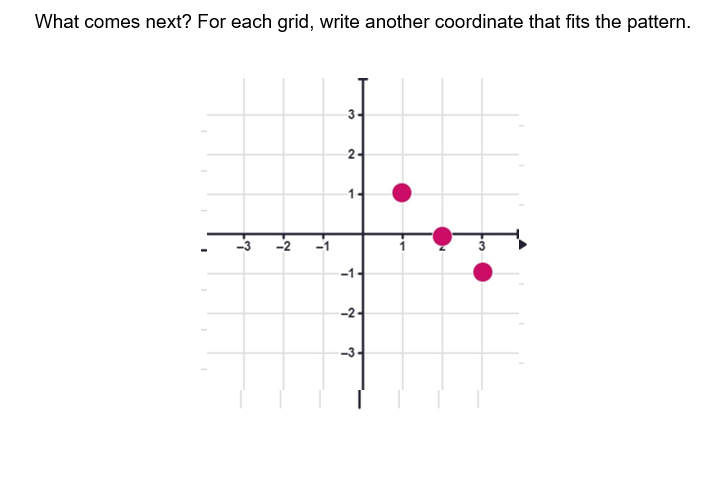
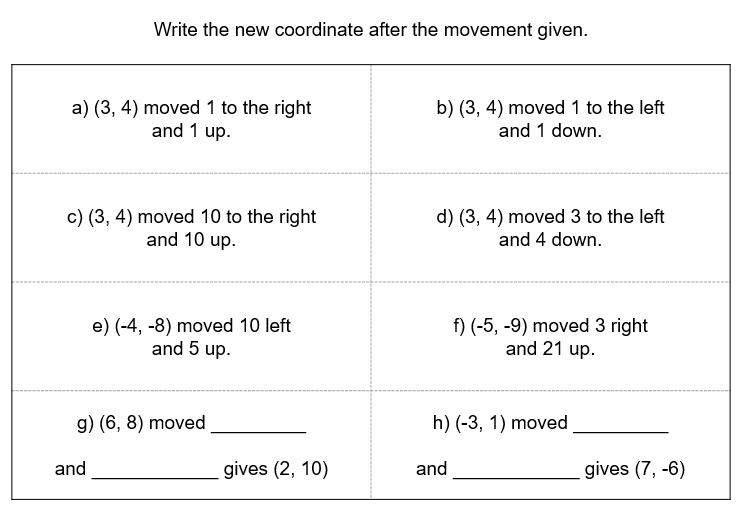
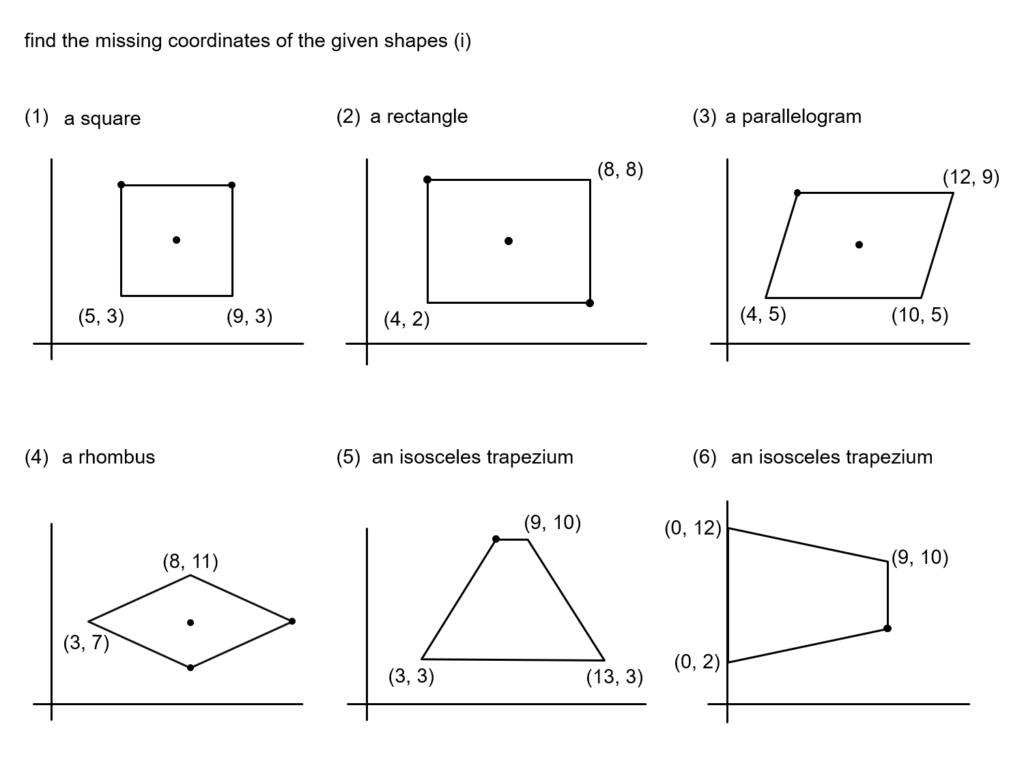
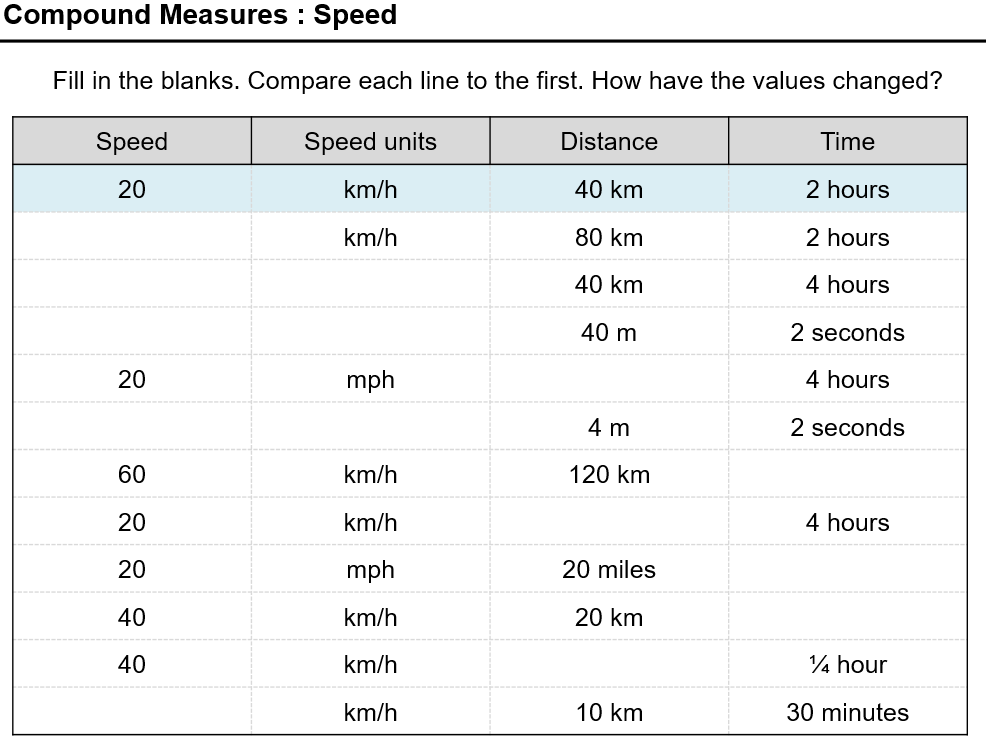
This is pretty simple stuff. But look at this example problem pair. It’s sideways!
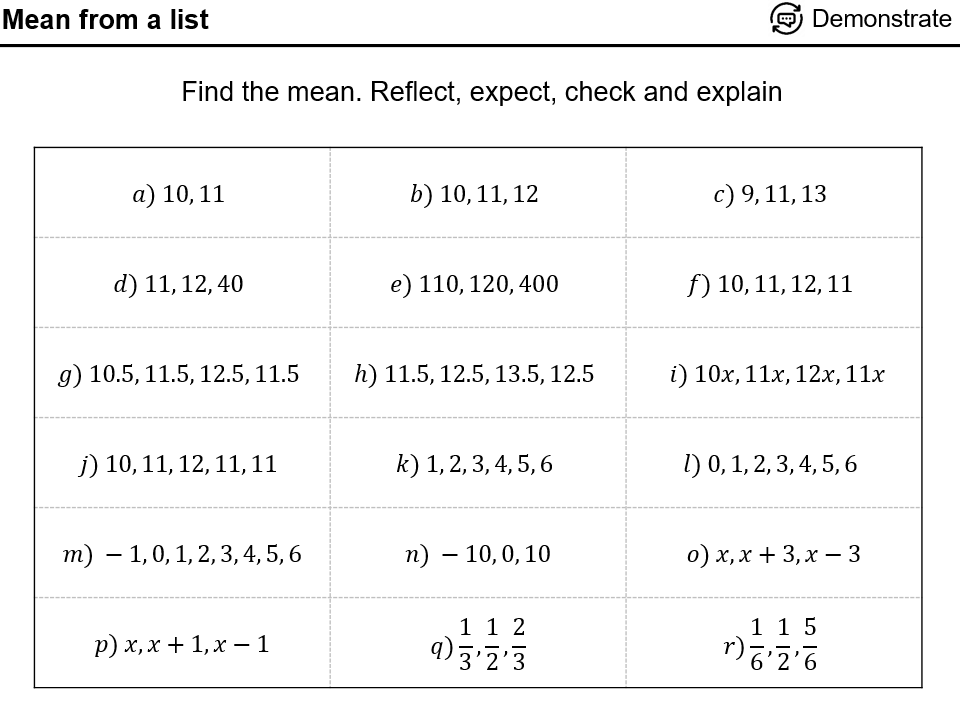
I think these are best printed off (2 per page) and stuck in books. They look quite nice like that.
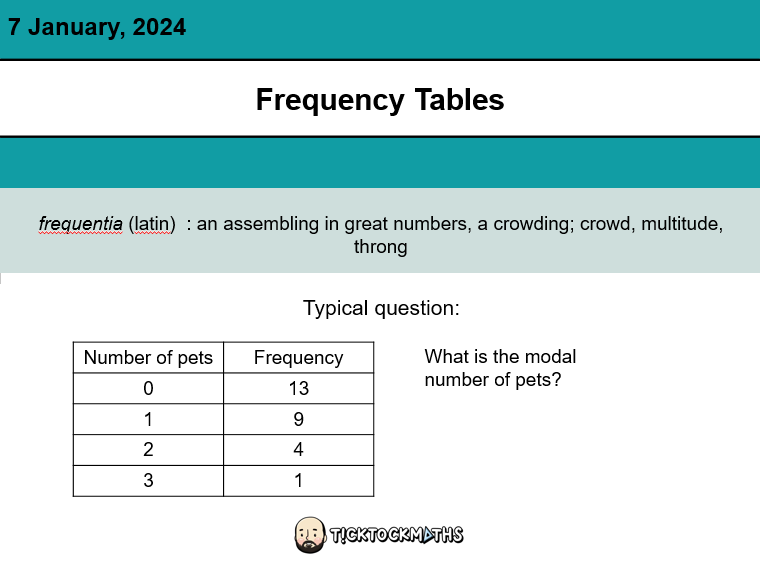
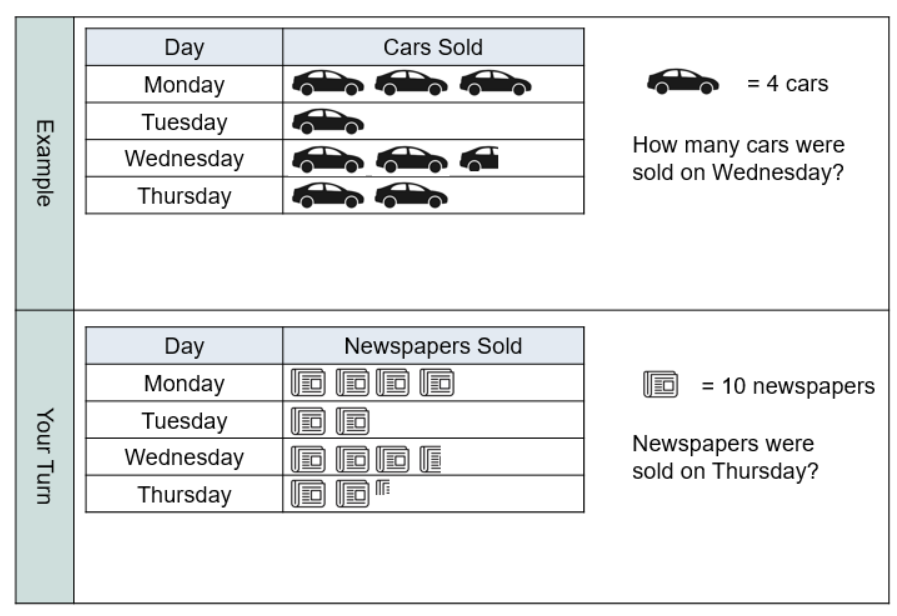
My exercise here is massive in debt to @GiftedHKO’s Pictogram work which is AWESOME. I’ve used some of the same ideas.
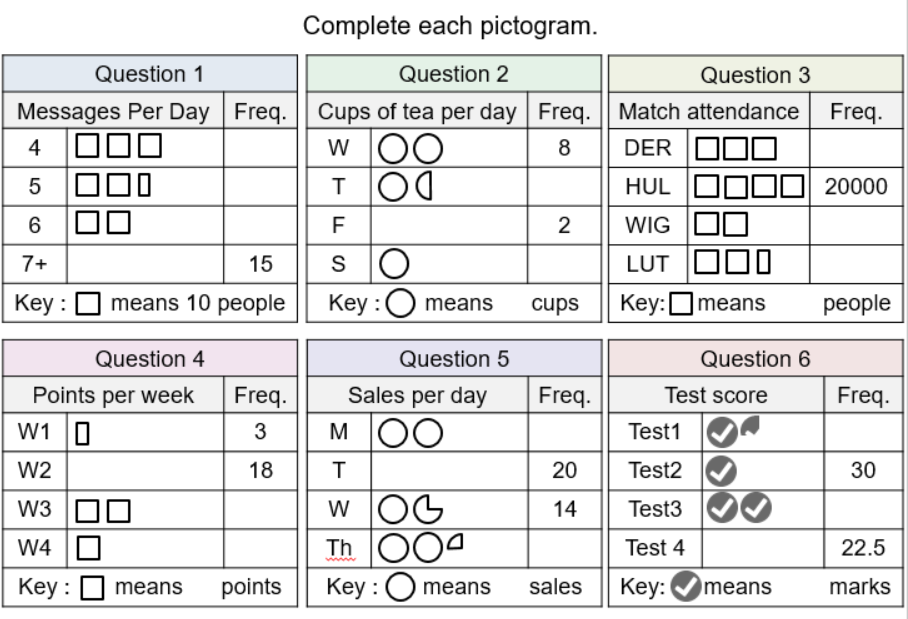
Then there’s the usual. A 5 quick question plenary and I’ve added in a lovely exam question as well, that requires knowledge of the mean.
***
A note here : this will probably be the last resource for a while, my timetable is going back to chocka this week. But that’s all of the Maths Genie grade 1 stuff ticked off.

I’m becoming happier with how content has been covered by the resources on the site. Use the menu at the top to see it all!
I hope I can cover all of Grade 2 by the end of the academic year and work towards full coverage. I don’t just want to do stuff for doing stuff’s sake, though. There are loads of good resources out there and I don’t want to just add to the pile without making mine have some sort of value or differentiator. I like to think through my own questions and build things properly. So it might take a while. And when I’m done, I’ll probably think it all sucks and want to make it all again. 🤷♂️