Made this lesson as I was due to teach it and I realised that my previous slides were stinky.
I’m quite proud of the questions.

Made this lesson as I was due to teach it and I realised that my previous slides were stinky.
I’m quite proud of the questions.


I think one of the reasons students struggle so much when facing this topic is the amount of ways we can phrase things. x multiplied by y. x times y. x lots of y. x items costing y each.
I’ve tried to collect some of these here, but I’m sure there are loads more!
This lesson is whiteboard heavy. It’s the best way, I think.
Students still found it hard. Sometimes with a topic like this, it’s hard to see why. We muddled through, but it didn’t flow as gracefully as it could have. I’d love some feedback/thoughts on this.
@ticktockmaths on twitter if you wanna chat, although I don’t know how much longer I can justify having a Twitter. All my audience is there. But it’s not a great place. I think I’m moving to BlueSky sooner rather than later.
Maybe FDP next. Maybe not for a while.
I collect bad graphs.
I used to keep them as a PowerPoint, but I thought I’d bring them together here as a slideshow. I did promise to do this a month ago. Sorry to @VVMinkov on Twitter.
Usually I present the graphs. Ask students to think for themselves for 30 seconds. Then talk to their partner to 1 minute.
I might ask : ‘Why is this graph bad? Do you think it is deliberately bad? If so, are the creators of the graph trying to tell a story? If not, what mistakes have they made?’
I will try and update this slideshow when people send me more bad graphs.
Click any image to launch a full screen gallery.



























(As a side note, I’d really like to not use TES to host these resources at some point, but haven’t really found a better option).
This is pretty simple stuff. But look at this example problem pair. It’s sideways!
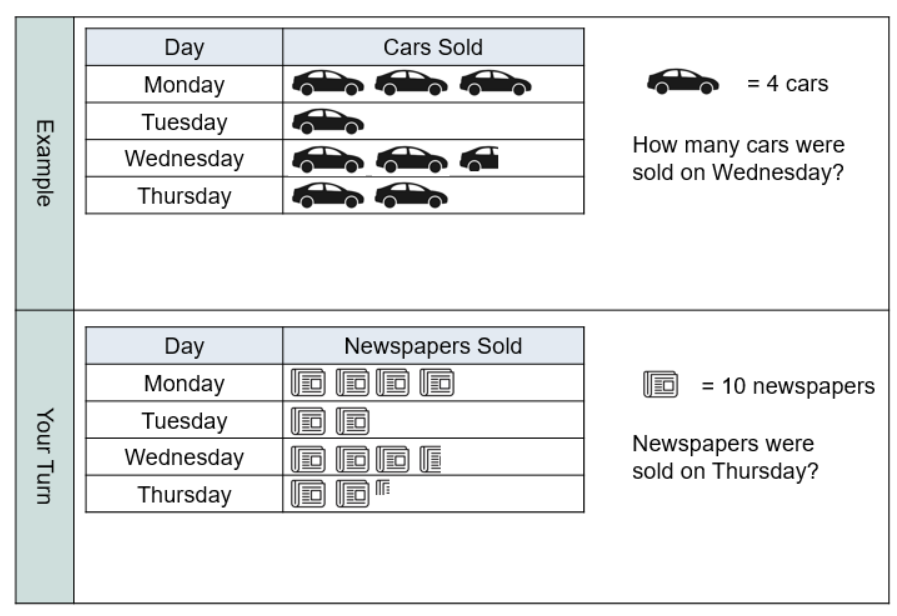
I think these are best printed off (2 per page) and stuck in books. They look quite nice like that.
My exercise here is massive in debt to @GiftedHKO’s Pictogram work which is AWESOME. I’ve used some of the same ideas.
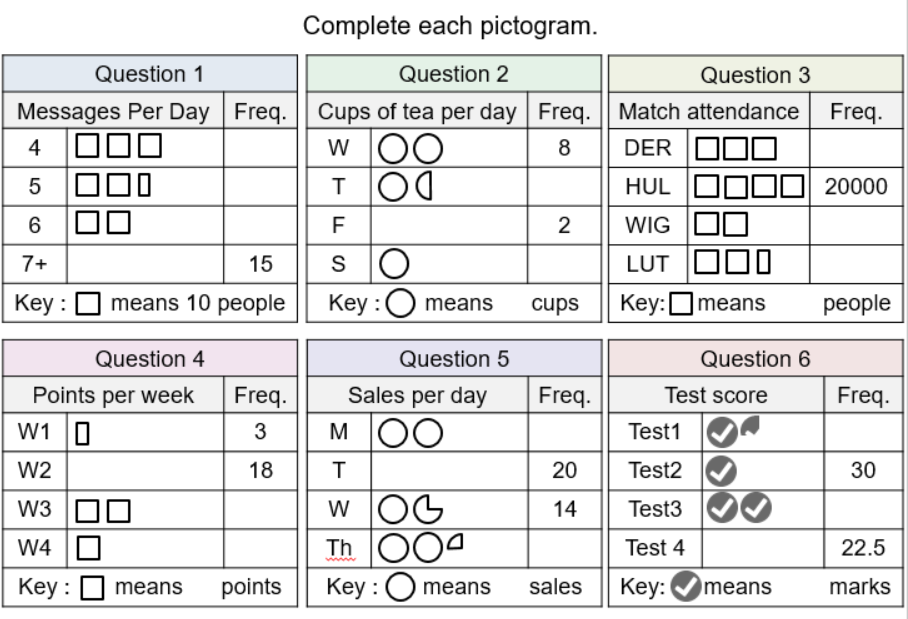
Then there’s the usual. A 5 quick question plenary and I’ve added in a lovely exam question as well, that requires knowledge of the mean.
***
A note here : this will probably be the last resource for a while, my timetable is going back to chocka this week. But that’s all of the Maths Genie grade 1 stuff ticked off.

I’m becoming happier with how content has been covered by the resources on the site. Use the menu at the top to see it all!
I hope I can cover all of Grade 2 by the end of the academic year and work towards full coverage. I don’t just want to do stuff for doing stuff’s sake, though. There are loads of good resources out there and I don’t want to just add to the pile without making mine have some sort of value or differentiator. I like to think through my own questions and build things properly. So it might take a while. And when I’m done, I’ll probably think it all sucks and want to make it all again. 🤷♂️
Download these resources here.
There’s actually a lot more to coordinates than is perhaps given space for in a lot of schemes of work.
I certainly have been guilty of skipping over the topic before, on the basis that the kids can ‘do it’ and have made trouble for myself later on down the line.
It’s not just about ‘along the corridor and up the stairs’. There’s the idea that a coordinate represents a position and is made up of an x and a y value.
I’ve tried to get a this here, but I slightly worry that I’ve mixed in too many ideas.

I’ve also hinted at straight line graphs and sequences with some mini-whiteboard work.
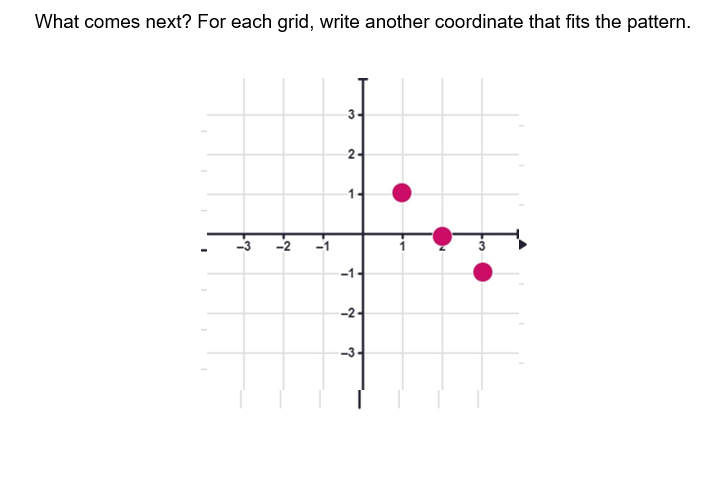
I’ve also talked about the MOVEMENT of coordinates.
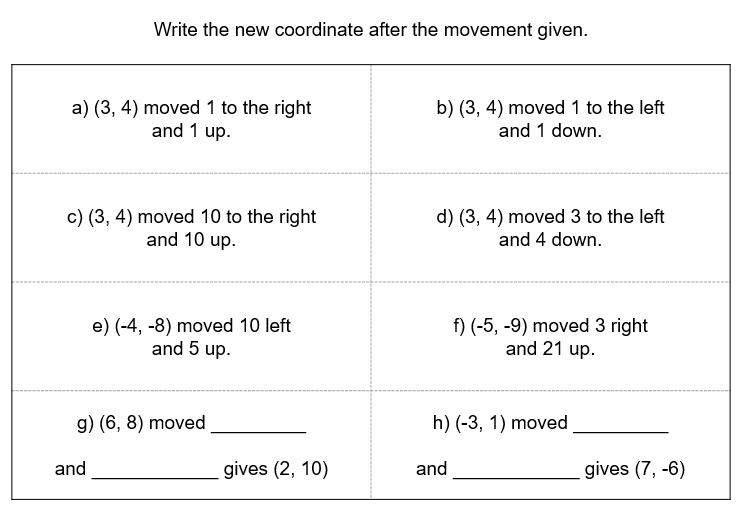
Manipulating coordinates and being comfortable doing so is, I think, important.
Hopefully this is packed with a lot more thinking that what I used to do early on in my career. Print off a sheet of some coordinates and ask students to read some and plot some. There’s nothing wrong with that kind of thing, but I’m not sure it should be the main event.
Similarly, I tried to make my plotting work a bit more involved.

The coordinate geometry slides are mainly about finding the midpoint.
But I did something I don’t normally do. I copied in the late, great Don Steward’s Quadrilaterals and Coordinates slides. Normally I write all my own questions, but these are BEAUTIFUL questions, and every classroom is richer for doing them.
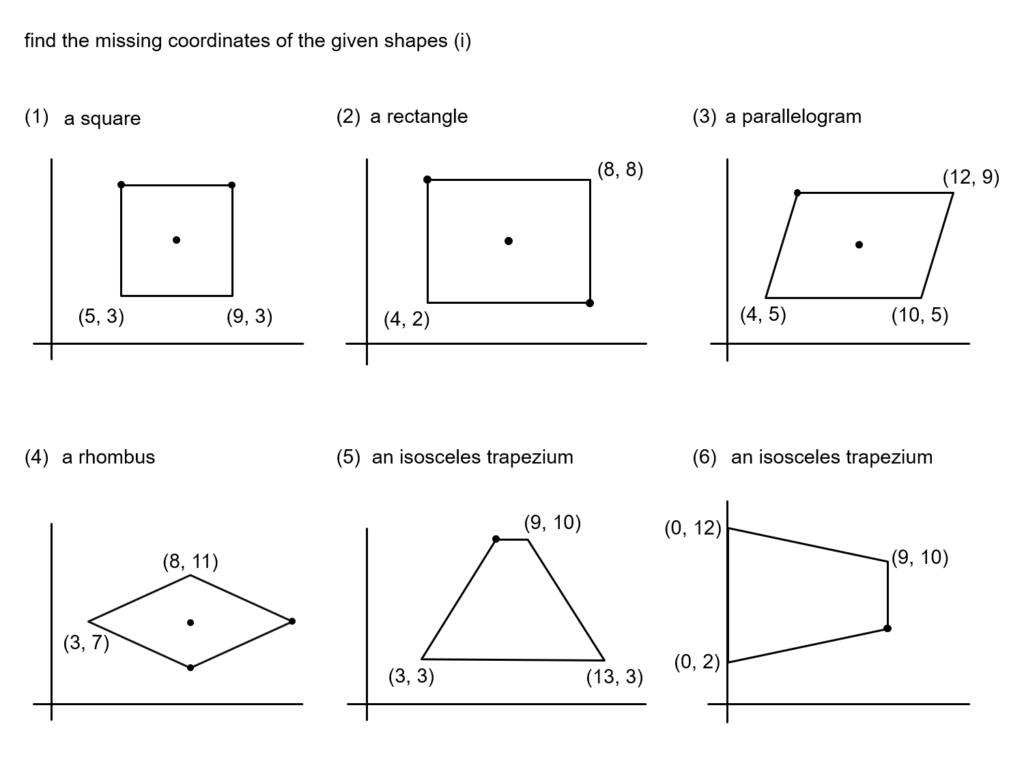
I had no way to add or improve on these.
If you are a member of Don’s family, and would like these slides removed, please contact me.
That’s all for now.
I just need to do some slides on Pictograms, and then the entire of MathsGenie’s grade 1 content is covered by TickTockMaths slides. I’m pretty proud of that, and hope to get to full coverage of up to grade 2 by the end of the year.
Rich
Hi all,
Last week I was busy. But not as busy as the week before. I finished off the negative numbers unit with
Ordering negative/directed numbers and multiplying and dividing negative numbers.
I also spent waaaayyy too much time organising the menu at the top of this page. Hover over it. Hopefully it’s more useful now.
Next up is coordinates and then pictograms. Coordinates is waaaay bigger than I gave it credit for. You could easily do two weeks worth of coordinate stuff.
Rich
So I had some free time last week and I decided to get some resources made/updated and published. Last week I published:
This year I’m going to try harder to get closer to more coverage with some of my slides. It’s a bit spotty at the moment. I’m going to be filling in gaps and getting stuff published, even if that stuff isn’t groundbreaking.
It’s always been in my eye to get full coverage up to GCSE. But that is a HUGE undertaking. It really makes you realise how CRAMMED with content the GCSE is, and how it does need scaling back a bit.
I’m closing in on Grade 1 full coverage. I just need to get some ordering negatives, multiplying negatives, coordinates and pictogram slides done. I know there’s no such thing as ‘grade 1 topics’, but I’m finding the Maths Genie list of topics useful and I’m working from that.
Anyway, I hope some of this is useful to some of you.
Rich
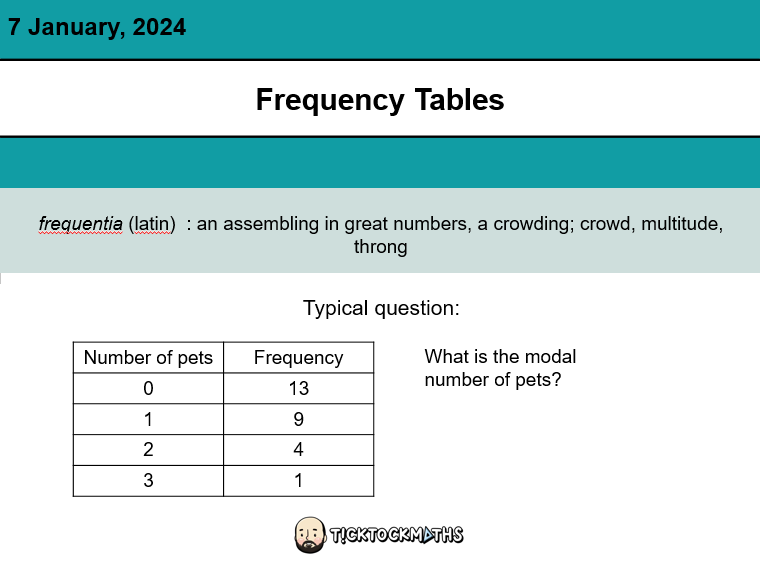
I’ve been avoiding putting this one up for a while, because I couldn’t think of any decent questions and this lesson is a bit all over the place. But it might be useful for someone. I swing between it not covering enough and it covering too much.
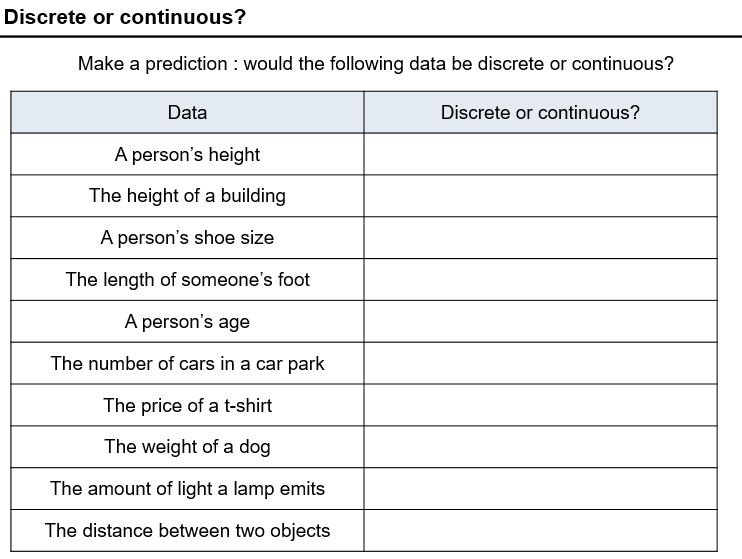
It starts with a variation theory thing on saying if a piece of data is discrete or continuous.
Then there’s some finding the mode from a frequency table example problem pairs and 4 (!!!) questions.
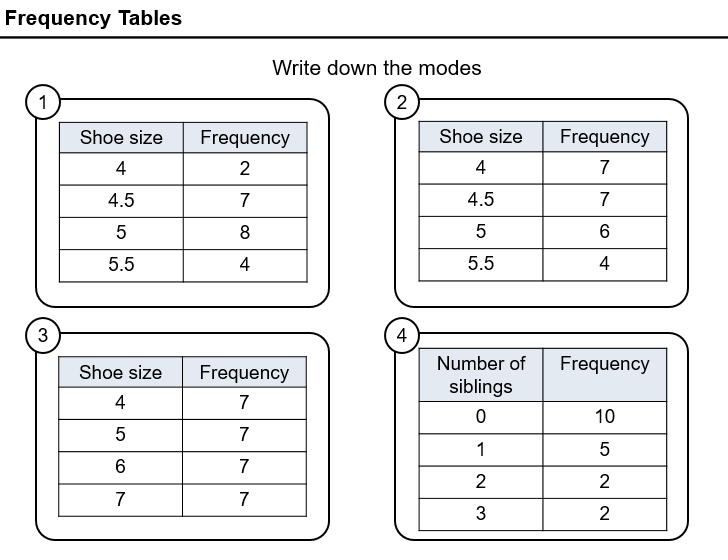
That’s my issue here. 4 questions isn’t enough. But I also couldn’t really think of any way to extend this and make it interesting. If you’ve got any ideas, tweet me @ticktockmaths, because really I could do with some more questions here.
Then there’s some example problem pairs on grouped frequency tables, and again, not enough and not interesting enough questions.
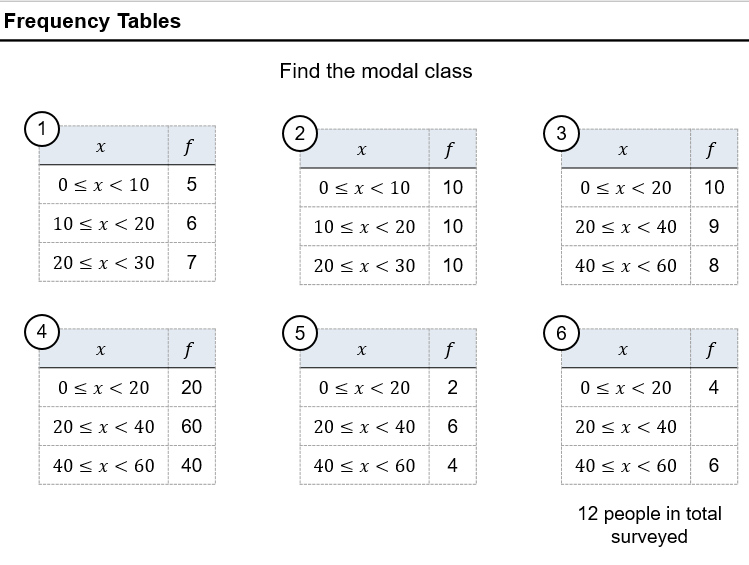
Then a plenary. Again, there’s not enough interesting here. Please get in contact if you can jazz this up.
Happy new year.
Rich

Download here : https://www.tes.com/teaching-resource/-12940897
Time flies. I realise that I’ve only uploaded one resource in the entire of 2023. That’s pretty bad going. I hope to be more productive in 2024.
This is a pretty simple resource about finding the gradient and y-intercept from an equation. But I wrote some nice questions.

Guess I’m just trying to get back into the swing of things.

That shape/space/measures bit of the menu is looking awfully bare. Not as bare as the data/probability section, but still.
Simple PowerPoint here.
Little starter
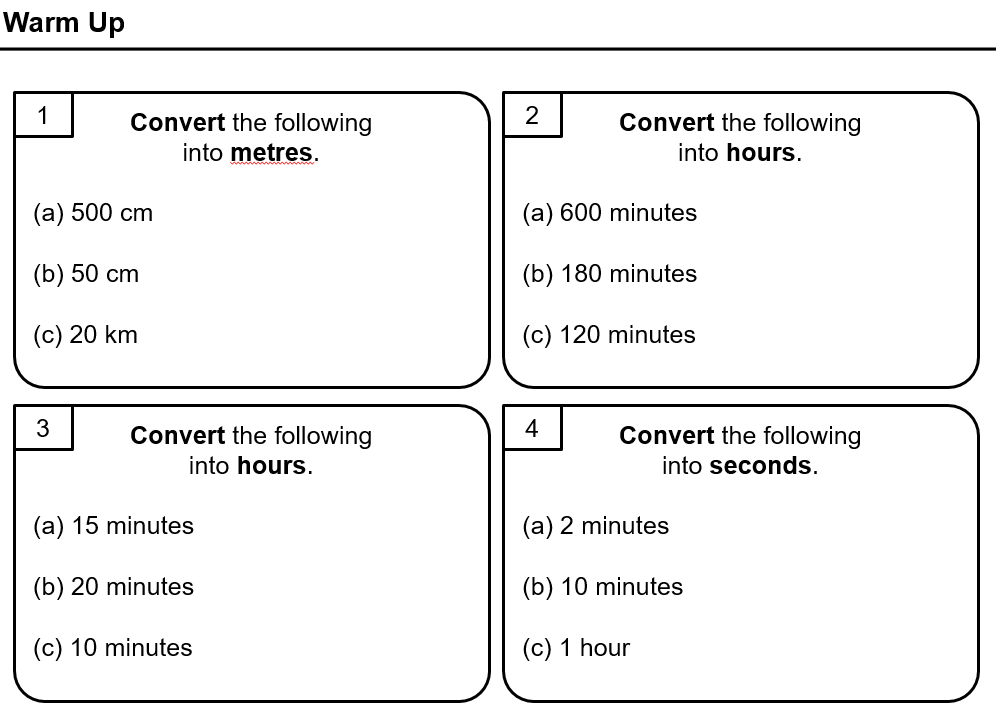
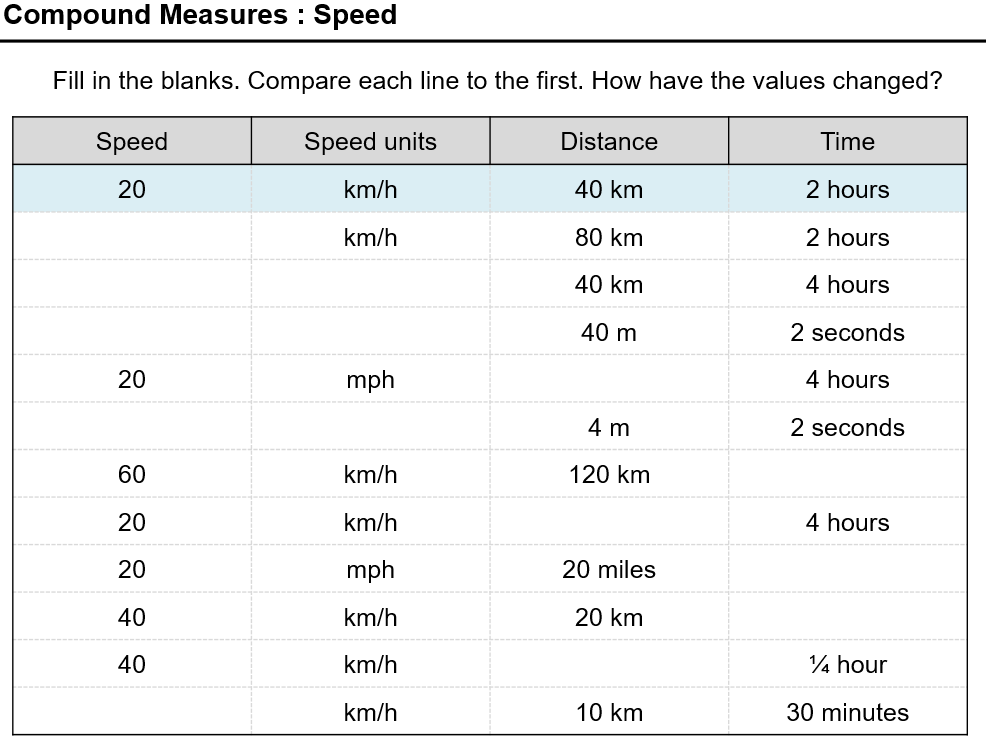
Not sure that the reflect/expect/reflect bit of these questions works. I’ve tried to make sure they compare it to the first question each time, but I think it is better when it’s more of a ‘journey’ and you compare it to the previous question in each case.
Still A* for formatting. It looks good.
Then I’ve made a blooket for some checking, some exam questions and a plenary.
This worked well with my group but it maybe needs some mini whiteboard work.
Have a lovely weekend
Richard