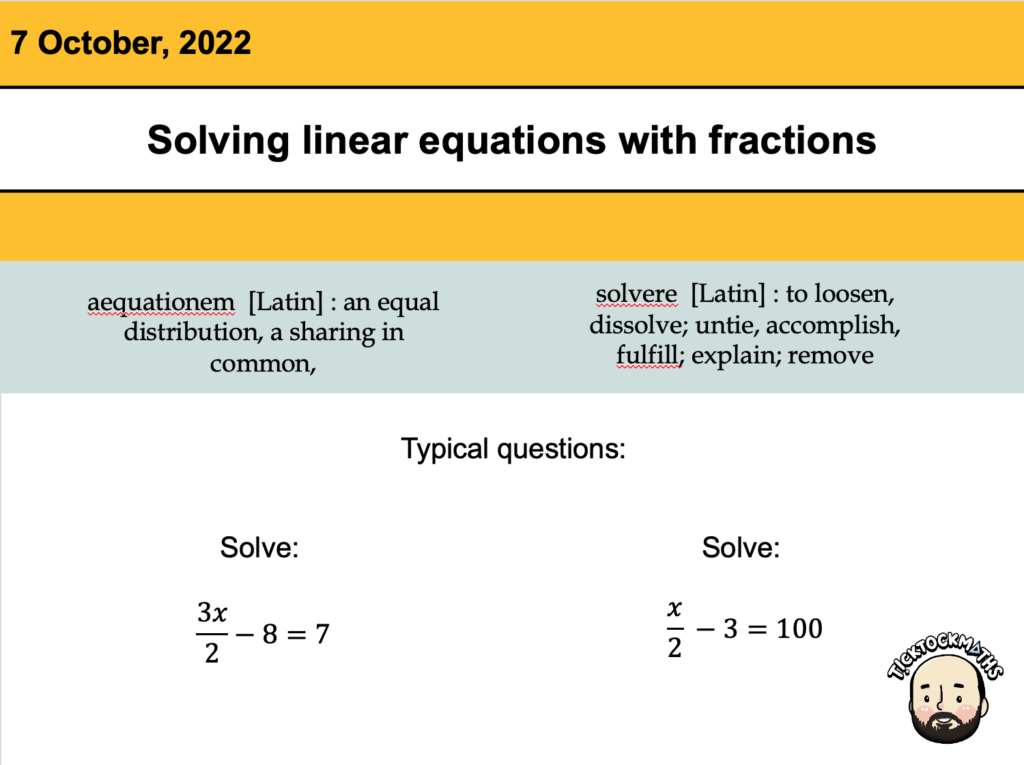
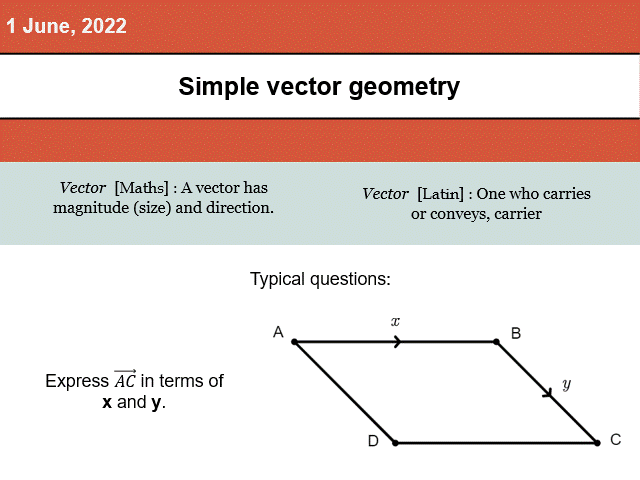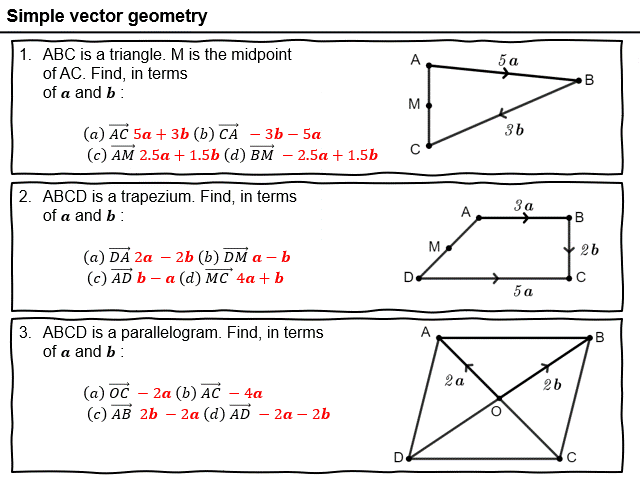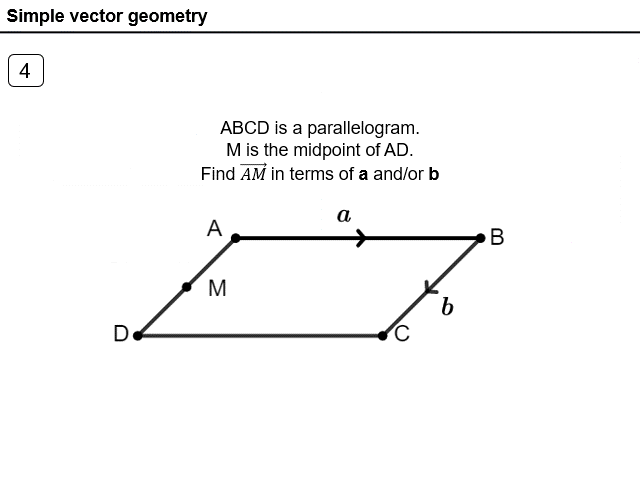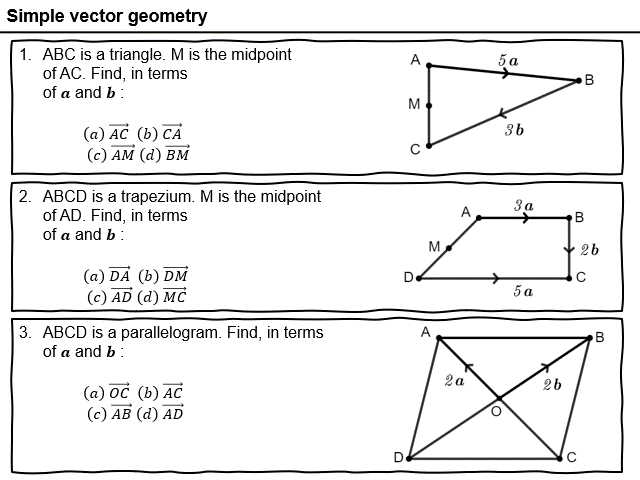
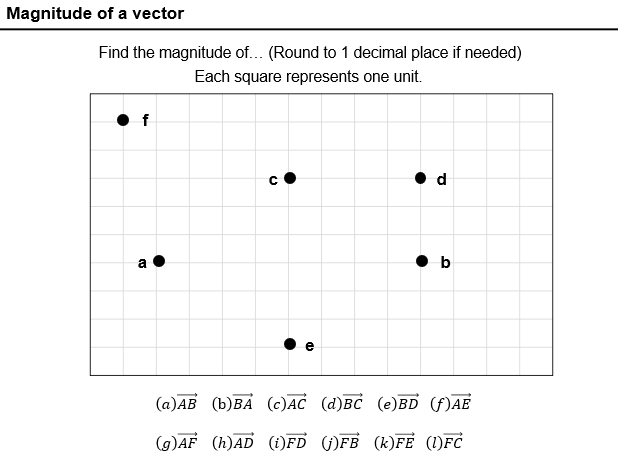
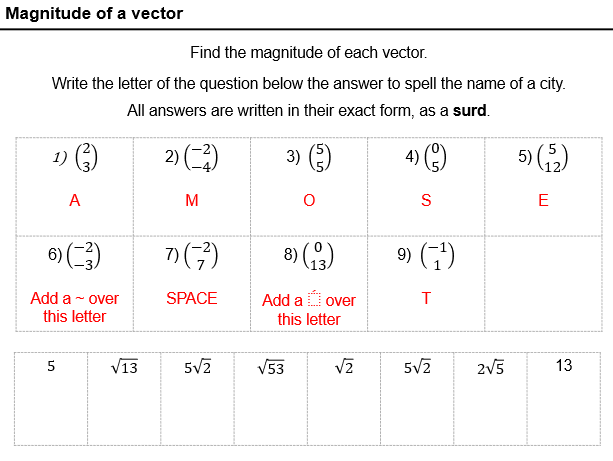
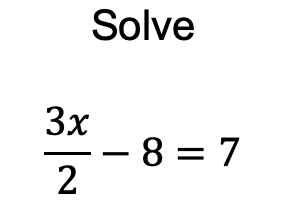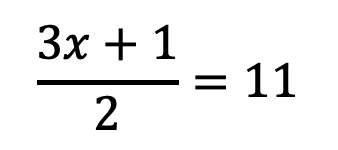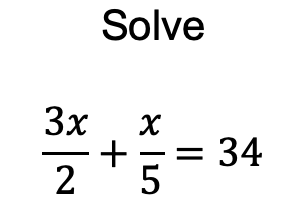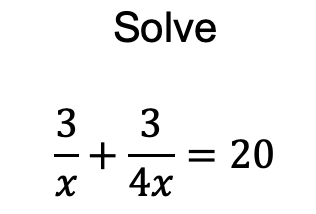Final resource of this half term.
I’ve packaged together some of the starters that I’ve been putting on Twitter challenging misconceptions I’ve seen in lessons. Stuff that I see a lot but doesn’t necessarily have a place in a SoW.
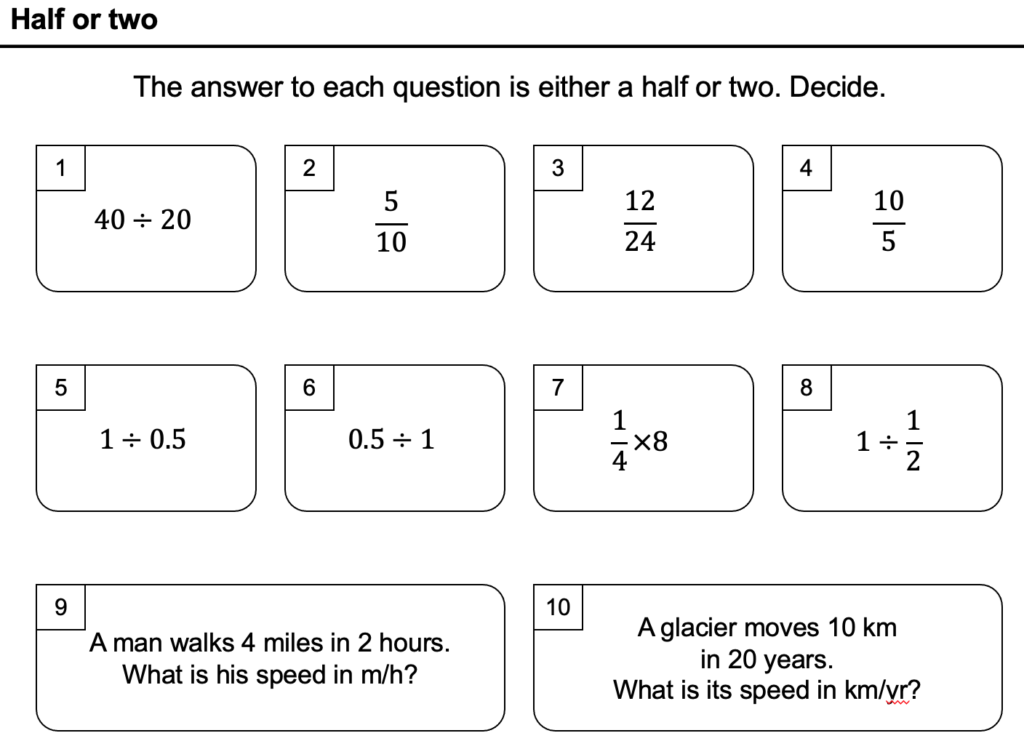
Stuff like the difference between a half and two
Or when we need to write trailing and leading zeroes.

I haven’t included the answers deliberately. These are meant for discussion. For instance, 12 here could be a currency.
I did the same with 1s.

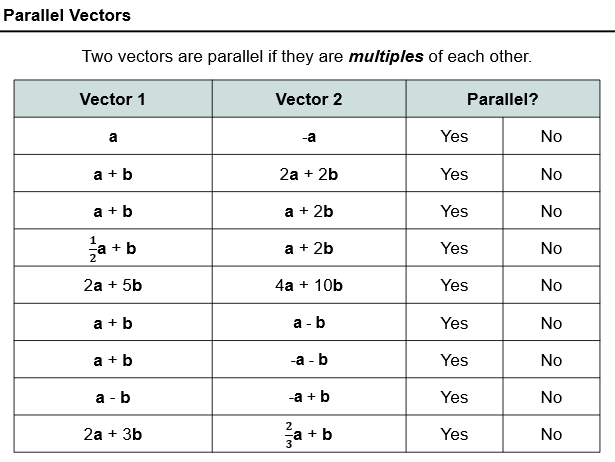
I would do these with any class that have had algebra introduced. Even doing it with my 11 Higher class caught some misconceptions.

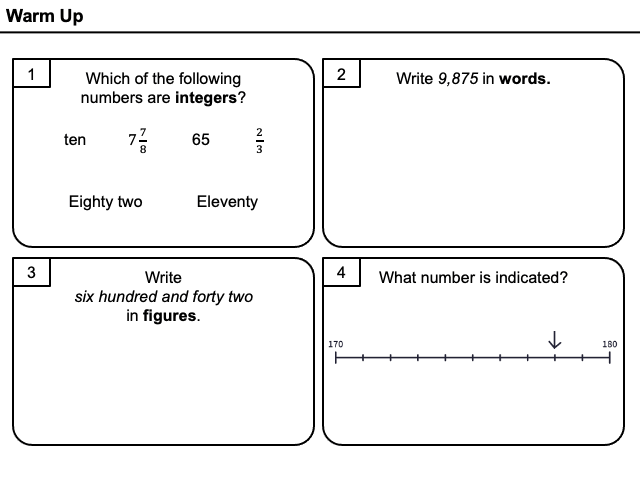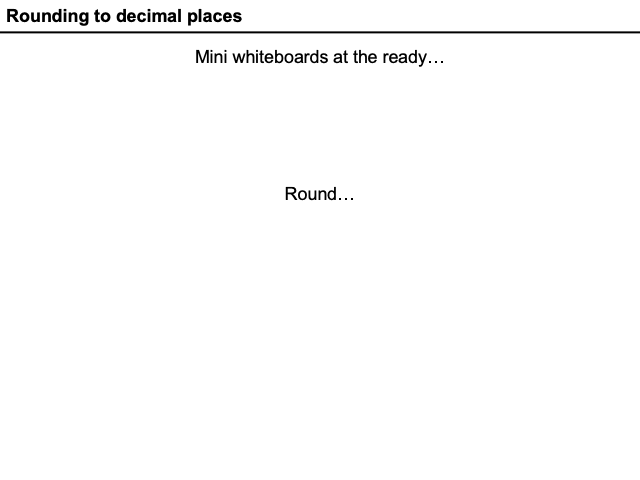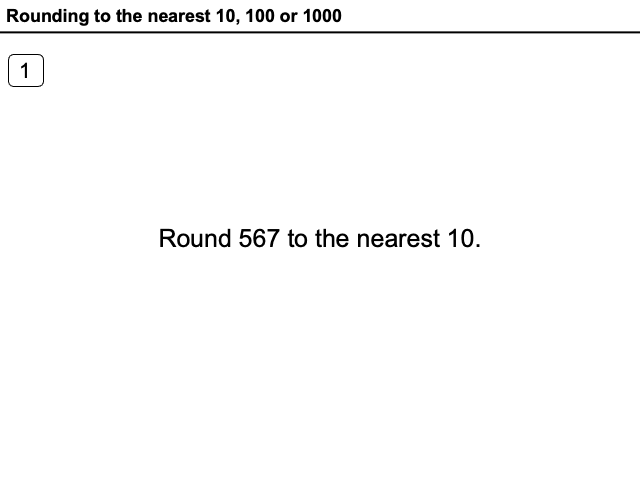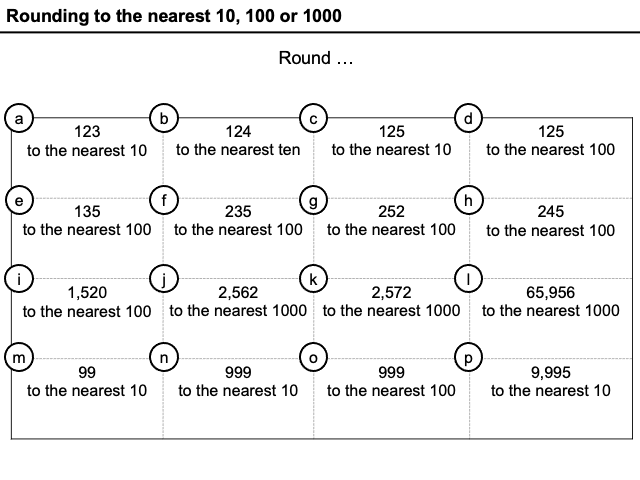
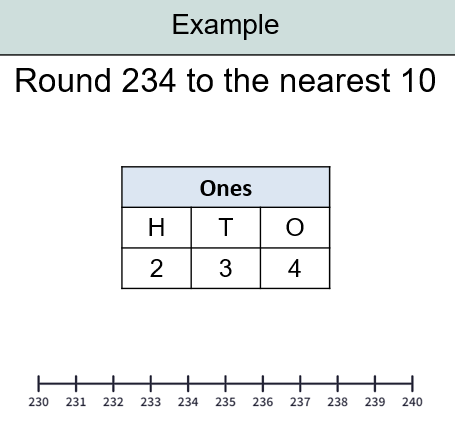
I would maybe only do this with lower years, though. I am trying to get at the idea that the digits stay in the same arrangement. I have found that I have two groups this year who find multiplying and dividing by 10, 100 and 1000 really difficult. On a recent assessment more than a few tried to do 2401/100 using the bus stop method.
I’ve reinforced it and reinforced it, but there are about 2 or 3 that still lack the skill and I’m running out of ways to address it. Any ideas to @ticktockmaths on twitter.
There’s also some that struggle with halving and doubling quickly. Again, really struggling to embed this.

This one tries to get at the unitary thing. It was interesting hearing student responses, especially as the answer depends so much on what x is. There’s a version with 3 if you want something more concrete.

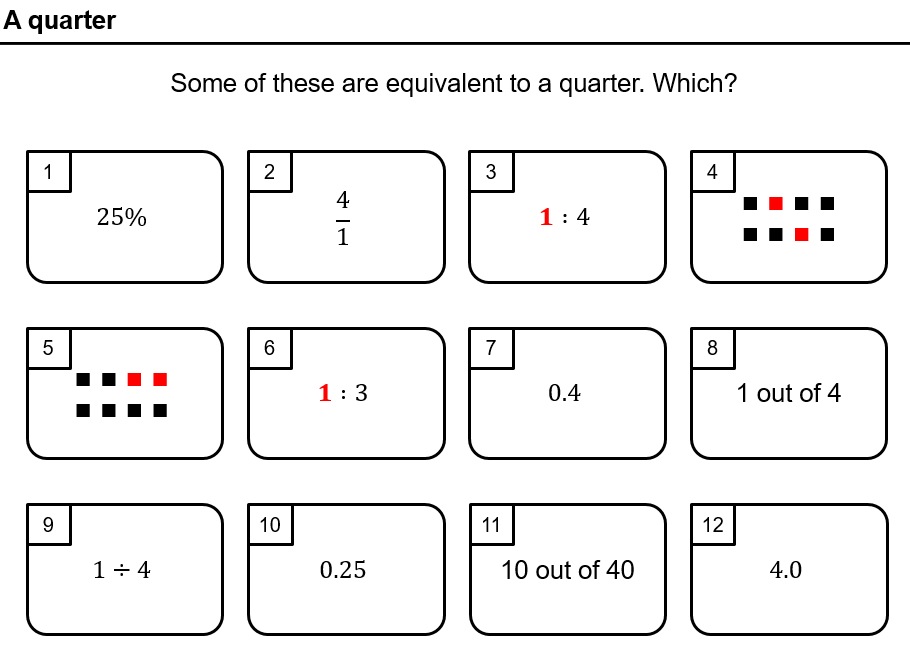
The last one is identifying if the answer is a quarter (like half or two. I was kinda losing steam by this point.)
Right, that’s it for this half term.
I’ve managed to fill quite a lot of gaps.
Behind the scenes I’ve also got a lot of PowerPoints half started, ready to be finished up and polished up for uploading here. The goal of covering most things seems achievable, if still long way away.
No resource next week. It’s half term and I want a rest.
Richard