Just a load of interesting (ish) ratio problems to work though.
I used bar modelling. I am increasingly into bar modelling for KS3, although I’m still not massively convinced when it comes to negatives.

I call these ‘reverse’ ratio problems. I don’t know if that’s the correct terminology.

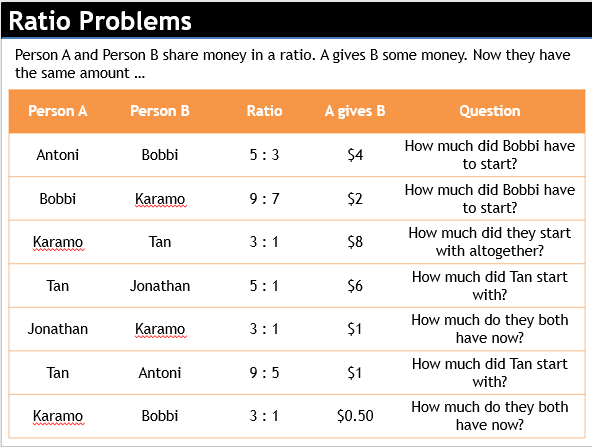
I have been watching a lot of Queer Eye recently.

I like bar modelling for questions like this.
Also

Some questions adapted from Don Steward and White Rose Maths Hub’s Barvember 2017.
No posts for two weeks now. I’m on holiday. When I get back, Pythagoras and Trig!
