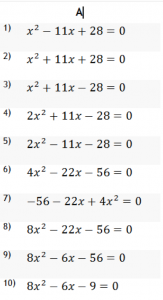Quadratic Simultaneous Equations

Here is a lesson on Non-linear simultaneous equations. Three example problem pairs. Some questions. Something a bit more problem solve-y. 5 timed questions. Some exam questions. It’s quite basic, really.

I know I haven’t posted much recently.

I will try and post some more stuff.

There’s a big difference between stuff to make for myself and stuff to publish. I usually just find some questions and paste them in for myself. Writing the questions and getting this up to snuff for publishing took a good couple of hours, and it’s quite a basic lesson.

PS I recently subscribed to MathsPad and it’s really good.

New Lesson: Using the quadratic formula

THE LESSON IS HERE.

This lesson was a massive learning curve for me and I’ve massively changed it after I taught my year 10s.

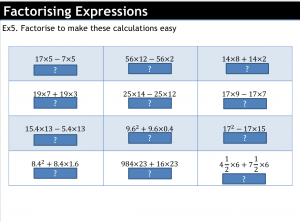
The first version of the lesson presented an example problem pair and asked them to get on with a variation activity. How hard could plugging numbers into a formula be? Well, it turned out the lesson was a little rubbish, and students really struggled.

After the lesson I got to thinking why.

I think I had not thought deeply enough about what can go wrong in the quadratic formula.

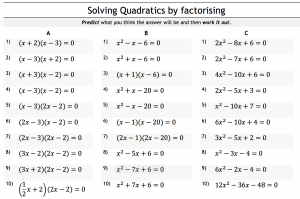
Specifically, I did not make it explicit enough that a, b and c contain not just the coefficients of x squared, x and the constant. They also contain their direction. In the equation x^2 -3x + 2 = 0, b is -3, not 3.

I wrote an activity to tackle this and added it in when I retaught it the following day. It went a lot better.

There was also confusion around a negative b going into the -b bit of the formula. It just shows, I’ve been teaching 7 years but there’s always stuff to learn and think about. Often things we think are straightforward are anything but to our students.

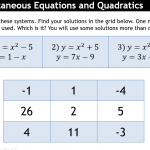
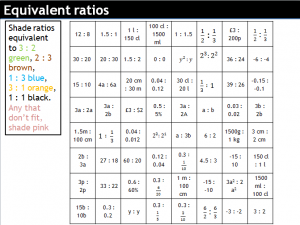
I’m also not sure how good the vary and twist activity is [available here].

I have split it into two sections on the PowerPoint, surely a sign it should really be two worksheets. However, I’ve still left it as one, for printing reasons.

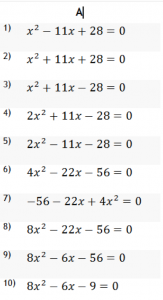
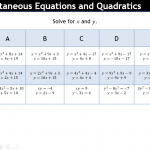
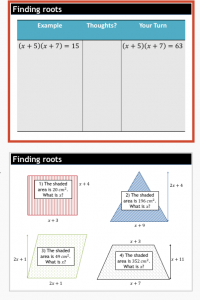
I also wrote some questions I thought were lovely.

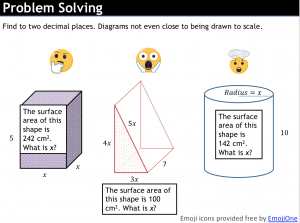
There’s quite a bit to discuss here. I like the emoji format. Does that middle question need to 5x on the diagonal? I don’t know if removing it makes the problem better.

These proved very challenging for students. I really should have scaffolded more, but I’m not sure how I could have without giving the game away and making the questions trivial. Some students liked these problems. Quite a few didn’t engage. It was hot and after break.

I’m still sharing the lesson here, with adaptations I’ve made. Maybe you’d like to make your own. Again, I’ve tried to go into more depth with things like the number of roots.

There’s also a set of timed questions here. Again, this is picking from a couple of thousand questions. It also picks from a database so you should never see repeat questions or nonsensical questions. I’ve done the four levels like so
Level 1 : Naming a, b and c
Level 2 : Solving a simple one
Level 3 : Introducing negatives
Level 4 : Number of roots

A long time project might be to adapt this resource so you can choose the number in each skill level to display.

Please comment with any suggestions.

New(ish) lesson: Factorising Single Brackets

THE LESSON IS AVAILABLE HERE

This isn’t completely new. I’ve edited and refined a lesson I’ve had on here before. Except I’ve packed it with MORE STUFF. I’eve tried to use Jo Morgan’s idea of going more in depth. So this lesson has:

Some I do you do/examples.

One of my vary and twist activities. Available as a word file here.

Some ‘does it fit’ whole class discussion. Look at question 4. Oh my!

A ‘spotting of mistakes’ activity to really hammer the point home.

Using factorisation to complete calculations. Yes please!

A problem solving task!

Oh. Then I thought. How about a plenary.

On the powerpoint is a quite nicely thought about 5 question mini test thing. It’s quite easy. But Craig Barton has defiantly managed to convince me that chucking a really hard question at the end is a mistake and maybe we should be giving students confidence at the end.

I know what you’re thinking.

What if I want some slop. Or some more timed questions? You can get some here. It randomly picks from…wait for it…over 2,000 questions!!!

Sometimes I think I should plan more lessons like this.

Including coding and stuff for the questions on the timed questions it took me about 5 hours.

Maybe that’s why.

As always give me a shout if I’ve idioted a question up.

Excuse me if the writing style was mad today. I downed a lot of Cherry Coke whilst coding.

Robert Low: Why is subtraction so hard?

Really interesting article and worth a read

Subtraction presents various problems to learners of mathematics, not least with the mechanics of hand calculating the result of subtracting one multi-digit number from another. But that’s not the kind of difficulty I’m interested in: I’m more interested here in the difficulties that arise when computations involving several additions and subtractions of integers are involved, or at the slightly more advanced level where algebraic computations involving several additions and subtractions are required. I’m going to take a look at what I think lies underneath the difficulty.

http://robjlow.blogspot.com/2018/06/why-is-subtraction-so-hard.html

New lesson: Finding roots of quadratics by factorising

This is my biggest set of lesson stuff yet.

The PowerPoint introduces the topic. It sets up some example-problem pairs.

It then leads onto some vary and twist questions, which are available here as Word file.

The PowerPoint then goes onto talking about solving when rearranged and includes a Victorian textbook exercise and some questions where you have to find x, given the area of some shapes (this took ages to do. I posted it to Twitter twice. Both times the questions were written wrong. Doh!)

I’ve also included an open middle problem solving thing and a timed learning check, that graduates in difficulty.

Talking about learning checks…I’ve also written some Timed Questions that increase in complexity every 3 questions. I now have over 6000 questions in my Timed Questions database!

As always, comment and critique.

There’s probably 2 lessons of stuff here, easily.

EDIT: One of the area problems was still wrong! Thanks to Professor Smudge for catching that 🙂

New Resource : Simplifying ratio timed questions

Like the old ten quick questions, but with three levels of difficulty.

Level one (first three questions) : Prime divisor

Level two (second three questions) : Compound divisor

Level three (third three questions) : 1 : n

Level four (last question) : Units

Tempted to extend it to do 12 questions. That last question feels odd on it’s own.

Also the PDF generation is weird. Think you have to click go for it not to be a blank page. And allow cookies.

I messed up the question generation code so had to go back in and manually edit hundreds of answers 🙁

Get it here.

Sometimes if you mess around with changing the id and sid parts of the url you might see stuff I’ve been working on but not blogged about yet. (Try 8,1 8,2 for instance )

New resource : Equivalent and Simplifying ratio lesson

Wrote this powerpoint today.

It’s like my ProjectALesson stuff but I’ve taken A LOT of explanation out. I’ve also got some stuff you need to print out. I’m not sure making them ‘pick up and go’ was that helpful.

It takes a lot of inspiration from variationtheory.com. It’s my new favourite website. It’s ACE.

I also took a lot of inspiration from Jo Morgan’s MathsConf session . She was talking about covering stuff in depth, and not missing an opportunity to go into negatives and fractions.

I made what is probably my favourite exercise of all time based on this. My colleague Mike helped me write the questions (Hi Mike!) and some of them are superb, although they might be a bit much/challenging. As an aside, sitting with my colleague and writing some questions was a great use of our time. Mike came up with some questions that I wouldn’t have. I love the misconception of 2^3 : 2^2 being the same as 2 : 3. Mike came up with that. It also made us discuss stuff really deeply. If you’ve got some gained time, write some questions with a colleague.

See what you think. As always, the discussion is the fun bit.

EDIT : I’ve uploaded this ‘Pixel Picture’ as word file on TES here. It makes the formatting a little nicer.

Updated resource: Collecting Like Terms Powerpoint

Doing teaching resources is hard! By the time you’ve written some, you realise what you’ve written is a little rubbish!

For instance, my ProjectALesson powerpoints need massive improvement. They often contribute to a modern epidemic in teachers : click-itis. I’ve seen this quite a few times. I’ve been guilty of it myself. I have no idea how to get around this, really.

One of the things I did whist updating my collecting like terms PowerPoint was to remove a lot of the writing. I think this was pointless anyway. It can’t have done anything other that overwhelm students with too much stuff on the screen.

I have added a little bit of silent teacher modelling in there, talking about which terms are like.

I’m not sure what to do, really. Update the old resources or make new, better, resources. Hmmmm.