OK. So this is a big one.
Firstly, I have found teaching negatives difficult in the past. Teaching the rules is a bit useless. ‘Two negatives make a positive’ often leads students to doing things like -5 – 9 = 4 (or similar). I avoid the rules like the plague.
I guess pattern spotting helps.

Here I have used a Craig Barton idea. The idea is that you present each set of examples, asking students to predict the result. You then wait during the … (the gap of understanding) and ask them to predict the result of the next one. Hopefully they see through pattern spotting what the answer is.
I’ve got some questions to support this.

I have tried to write questions that help develop student’s strategies like grouping.
Notice at this point it’s still all addition.
Increasingly I have found, however, that multiple representations are helpful. I used to think that I didn’t want to complicate things in student’s minds, and that showing differing methods would confuse them.
I’m now of the opinion that switching between multiple representations is really, really useful. Students who can do this are much more successful and I’ve tried to be more explicit in adding in differing representations into my work.
This is an idea I took from the excellent Pondering Planning website.
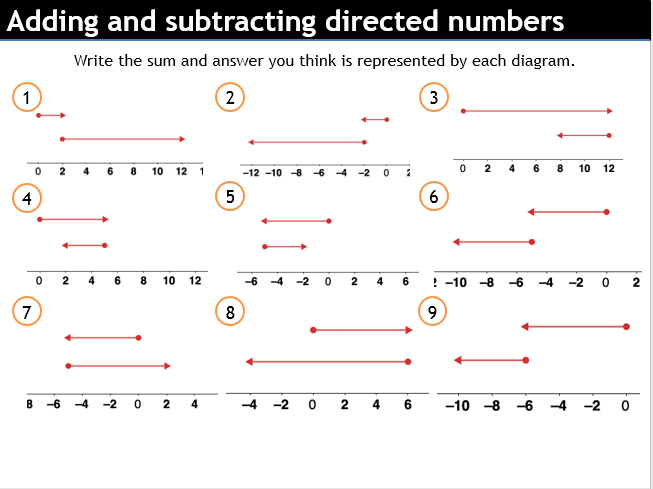
Notice I’ve done this AFTER the questions. I think sometimes it’s helpful to get students being able to solve the problems first and then supporting understanding later.
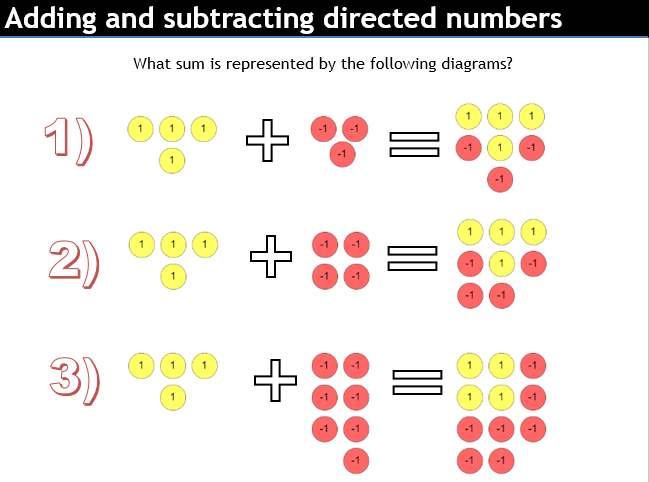
Even more representations!
I like double sided counters for negatives. They fall apart when multiplying or dividing by a negative, but they’re a useful representation for supporting addition and subtraction.
Hopefully, having differing representations helps students do some worded questions. I think this is probably a nice time to break for a lesson.

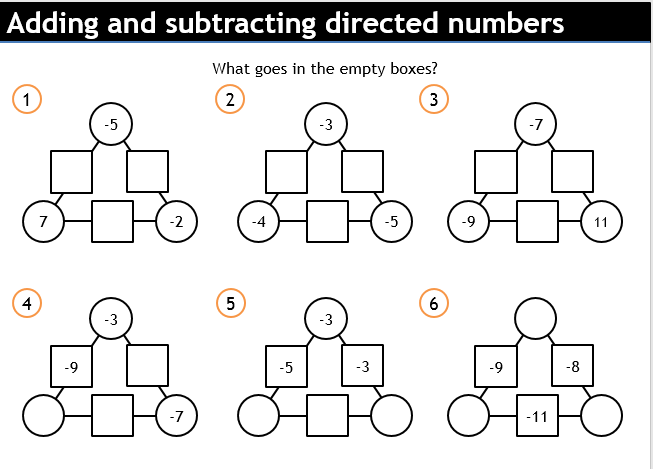
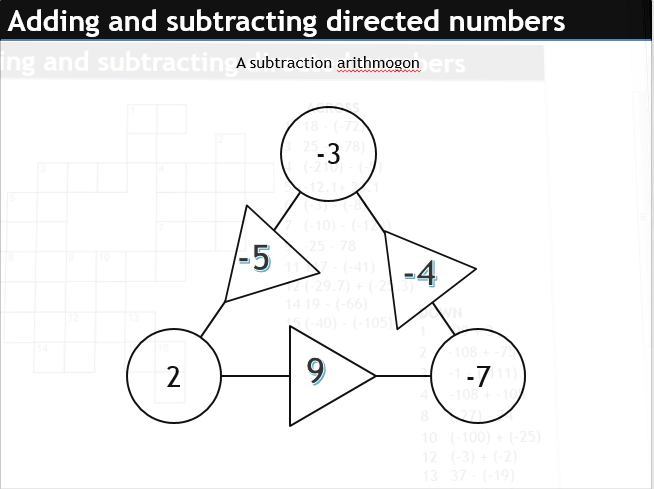
When we come to the second lesson, we could start by trying some arithmogons. I like arithmogons. They feel ‘puzzly’. The numbers in the box is equal to the sum of the circles either side. They test a bit of fluency.
Time to move on to subtraction using a similar frame. Including more patterns, questions and representations.
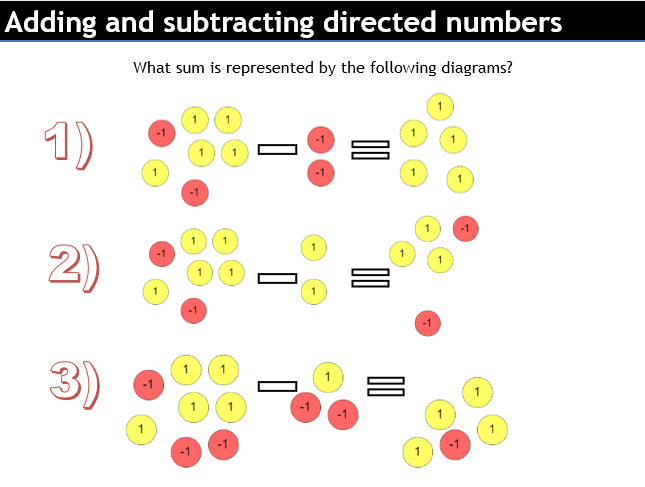
These questions tend to come up a lot in SATs.

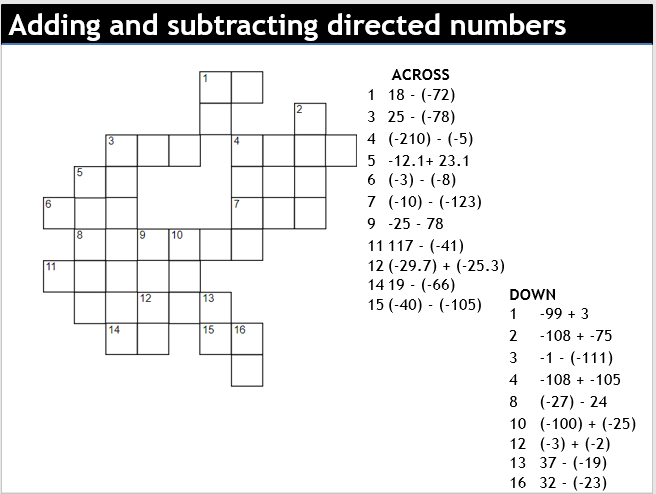
I even chucked in a crossnumber.
How about some negative arithmogons? You subtract along the direction of the arrow.
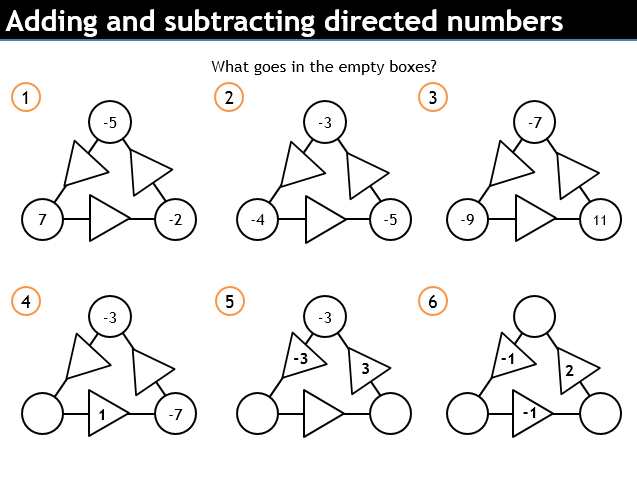
Maybe a little complex. I’ve written a sheet of them, though.
And of course, JMC questions often bring out a little understanding.

This is a pretty massive PowerPoint. 41 Slides. Probably 4 lessons. I don’t think I devoted enough time to doing negatives, before, though. This is pretty exhaustive.
Add a comment if you’ve got any suggestions for improvements.
